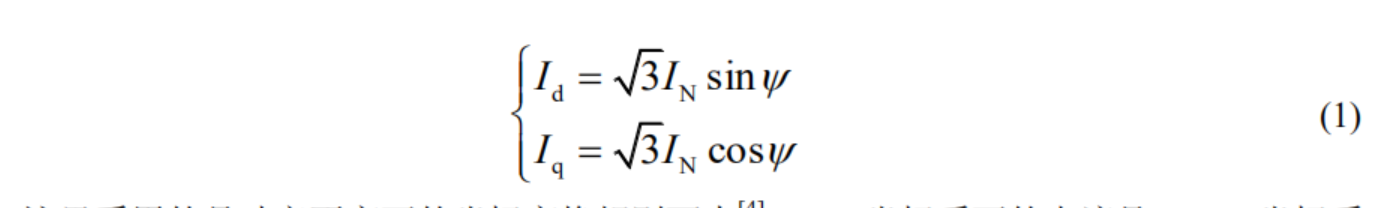引言
作为永磁电机的一种,内置式永磁同步电机(
上海合愉电机)由于其高转矩密度、高效率、易维护等特点被广泛用于各种场合。但是永磁同步电机也存在一些不同于电励磁电动机的问题,其主要原因是由于永磁体的引入,使得电机内电磁场的分布和性质都发生了很大变化,给分析、设计和研究提出了新问题。其中,电抗参数的准确计算就是重要问题之一。电抗参数计算的准确与否直接关系到电机的运行性能,并且,永磁同步电动机电抗参数的准确计算对控制算法的实现也有重要的影响。一般计算电抗参数的方法主要通过分别计算电机的交直轴空载场和负载场,通过这两个磁场的计算结果再分别计算交直轴电枢反应电抗,但该方法没有考虑永磁同步电机交直轴共磁路对电机电抗的影响,所以这种忽略交叉饱和影响的计算方法并不准确。因此,本文在考虑交叉饱和的情况下,以有限元的方法计算了电抗参数。
定子三相电流和交直轴电流的坐标变换
计算永磁同步电机(
合愉电机)的交直轴电抗参数,首先要知道交直轴电流,交直轴电流(
J238-7242)可以通过电机的额定电流 IN(相电流有效值)和内功率因数角 ψ(即合成电流值超前交轴的角度)得出
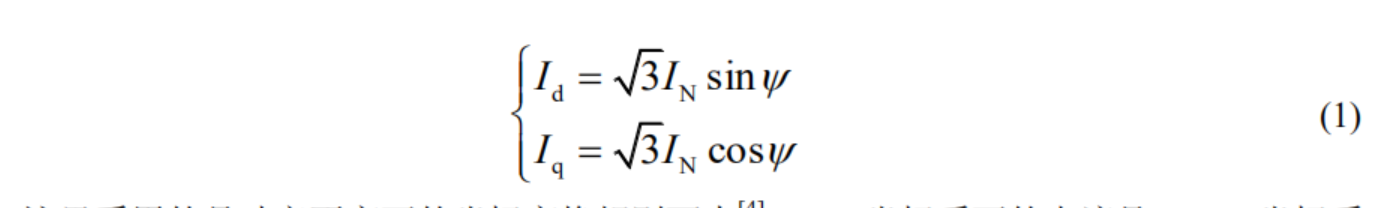
这里采用的是功率不变下的坐标变换规则而来,dq0 坐标系下的电流是 UVW 坐标系下的√m倍(m 为相数),三相系统中即为√3。因此为确保变换前后一致,在计算 Id、Iq时应在 IN 的基础上乘以√3,即按照上式的方法进行计算。以有限元方法计算电机电抗时,需要在所建立的模型中加以三相电流,通过 dq0 反变换可得到电机的三相电流,如式(2)所示。其中,θM为电机转子 d 轴与 U 相绕组轴线的夹角。
2 不同转子磁极结构下的内置式永磁同步电机电抗的研究
2.1 电机模型的建立
在 Ansoft 软件中建立了 V 型、V 一型、双 V 型三种不同的转子磁极结构电机的二维静态场模型,如图 1 所示。将已建立好的电机模型分别设置在二维静态场(即 Magnetostatic 模块)与二维瞬态场中(即 Transient 模块)中。在二维静态场模型中加以电感矩阵来计算三相电感值。研究以保证磁通一样的情况下,来比较不同转子磁极结构的电抗特性,根据公式E=4.44NkNfΦ,在绕组匝数、绕组系数、频率一样的条件下,即保证空载反电动势一样的情况下来比较不同转子磁极结构的电抗特性。(研究中将空载反电动势的值定为额定状态下的相电压,此电机额定相电压为 107V)
2.2 不同转子磁极结构下的电抗计算与分析
在 Magnetostatic 模块中计算得到电机的电感矩阵 Luvw,利用公式(3)至(5)的 dq0变换电感矩阵公式计算永磁电机 Ld、Lq、Ldq、Lqd参数,并利用公式 Xd=2πfLd,Xq=2πfLq计算交直轴电抗值,再通过 η=Xq/Xd计算得到不同转子磁极结构的凸极率,得出数据如表 1 所示。其中,Ld 为直轴同步电感,Lq 为交轴同步电感,Ldq 用于反映交轴电流对直轴电感的作用,Lqd用于反映交轴电流对直轴电感的作用。
通过对三种不同转子磁极结构电机电抗的研究,得出以下结论:
1.由于内置式永磁电机中永磁体的存在,永磁体磁导率很小接近于空气,交轴磁路的磁导要比直轴磁路大的多,因此交轴电抗要大于直轴电抗,这是内置式永磁电机区别与表面式永磁电机和电励磁电机的特点。
2.对于定子结构相同,在保证空载反电动势一致的情况下,对于内置式永磁同步电机而言,V 一型转子磁极结构的电机交直轴电抗值最小,双 V 型转子磁极结构的电机交直轴电抗值最大,V 型转子磁极结构的电机交直轴电抗介于两者之间。
3.在凸极率上,V 一型的转子磁极结构拥有最高的凸极率,可以产生最大的传动效率,双 V 型的转子磁极结构凸极率最小,在机电能量转换的过程中,效率不高。
3.电机饱和与永磁体结构参数对内置式永磁电机电抗的影响
随着电流 IN 的增大,电机凸极率开始降低,这对于内置式永磁电机利用磁阻转矩是不利的,因此在电流过大时,电机的机电能量转换效率也趋于降低。同样,观察数据可得出,在额定工作点附近(所采用电机额定电流 IN=84A),电机的凸极率
是最高的,电机效率最高、运行性能最好。
4 结论
本文对内置式永磁同步电机(
上海合愉电机)的电抗进行了研究,利用 Ansoft 电磁场软件以有限元分析的方法对 20kW、4 极 48 槽的内置式永磁电机进行了电抗计算与分析。首先研究了 V 型、V一型、双 V 型三种不同转子磁极结构电机电抗的区别与特点,再以 V 型转子磁极结构的内置式永磁同步电机为例,研究了电机饱和程度不同情况下电抗的区别与特点以及不同转子磁极位置的电抗区别与特点。