机电产品面向拆卸回收的绿色设计

可拆卸性设计是绿色产品设计的主要内容之一 ,它要 求在产品设计的初级阶段将可拆卸性作为结构设计的一个 目标 ,使产品的连接易于拆卸 ,并在产品废弃后可重用部分 得到充分的再利用 ,达到节约资源保护环境的目的 .然而 , 如何能反映产品拆卸所需要的特征 ,又便于拆卸路径的规 划; 既直观地反映产品的结构 ,又便于与 CAD集成; 既能 使计算机自动采集信息 ,又要拆卸方法简单 ,是摆在我们面 前的一个重大课题 .因此 ,建立一个什么样的拆卸回收结构 模型 ,就成为研究面向拆卸与回收的绿色设计的关键技术 .

用图来表示产品结构的装配关系是建立 机电产品拆卸与回收模型最常用的一种方法. 这里假设产 品的拆卸是装配的逆过程 ,产品结构的装配信息可由 CAD 软件包提供.信息主要分两类: 零件名称 ( ID)、零件联接方 式、零件与零件之间关系的类型 .设无向图 Gc= ( V , E) ,表 达的含义如下: 顶点 V代表零件或部件 , V = {ν1 ,ν2 ,…νn } ,其中 n为零 件的数目 ;边 E 代表一组装配关系 , E = { e1 ,e2 ,… em }, m代 表 边的数目 .若两个零件 νi 和 νj (νi ≠ νj ) 有边联接 ,则 (νi , νj ) ∈ E ,否则 (νi ,νj ) E.图 Gc 是一个无向图 ,而零件的顶 点 包括它的名称、重量、配合类型这些信息. 由紧固关系组 成的边含有紧固件的数量、紧固类型 ,紧固件指拆卸方式等 信息 .令 Ec = [Eij ]是 Gc 的邻接矩阵 , r i、 c i (i = 1, 2,… ,n ) 是 Ec的行向量和列向量.因为 Gc 是一个无向图 ,所以 Ec是 一个对称矩阵 .就有 r i = c t i (i = 1, 2,… ,n ) ,根据图论知识 可得:

2. 2 拆卸路径的规划

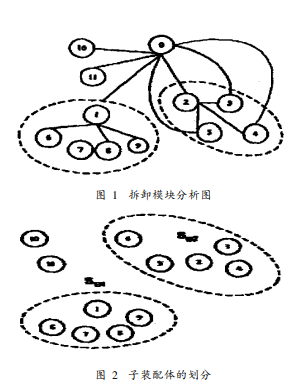
拆卸路径规划的方法有多种 ,这 里介绍的这种拆卸规划方法运用的是拆卸树的思想 ,其规 划思路为: 利用割点将产品分解成几个子装配体 ,以简化拆 卸的过程 ;对拆卸优先顺序评估 ,不论零件在此过程成中是 否 能拆卸 ;构造拆卸树 ,生成拆卸序列 .根据割点选取的原 则一次只能选取一个点作为真正的割点.在这里 ,割点就意 味着它是产品中的一个联接件 ,产品要想被拆开必须先拆 这个零件 ,也只有拆除这个零件产品才能被分解成若干个 独立的零件和子装配体.在图 1中 ,C0是最复杂的割点 CV , C10和 C11是两个悬挂点 ,其余的点就组成了图 G′ c = ( Gc - CV - C10 - C11 ) .进一步分析图 G′ c ,从深度搜索程序中可判 断出 G ′ c由两个子装配体 SB 1和 {C1 ,C6 , C7 ,C8 ,C9 }和 SB2 = {C2 ,C3 ,C4 } 组成 .

根据启发式搜索策略 ,分析出哪 个顶点作为割点 (最复杂的割点 CV ) ,可把产品的无向图 分解成若干个子图 ,在子图中寻找新的割点 ,不断地将子图 分解成更小的子图 ,这个过程就是拆卸规划的过程 .在拆卸 规划过程中 ,要明确拆卸的先后次序 ,这就存在拆卸优先矩阵的问题. 拆卸优先矩阵被定义为: 若一个零件妨碍另一 个零件的运动 ,则前者优先后者被拆除 .这种优先关系适合 于有相互联系的零件之间 ,可以确定一部分拆卸的顺序 .图 1所示结构在 6个方向上的拆卸优先矩阵可统一写成:

上海合愉对于相互关联的两个零件 ,它们在拆卸时存在着先后 的 顺序. 有些学者提出 ,在描述产品零部件的装配 (拆卸 ) 关系时 ,用有向线段来表示零件与零件之间的拆卸先后关 系 ,则可以大大提高拆卸规划的效率. 3. 1 以有向图作为拆卸回收模型的数学基础 定义一个 有向图 G= ( X , T ) , X = ( x 1 ,x 2 ,… xn ) 代表有向图中的节 点 ,它们表示装配体中的零部件. T = (t1 , t2 ,… tm ) 代表有 向图中的边 ,边表示节点之间的关系 ,插入一个有向图及它 的矩阵 .指出任意两点之间存在的通路个数 ,表明这两点之 间可能的拆卸路径 .我们仅仅知道任意两点之间的可能的拆卸路径是不全面的 ,它不能回答最先拆卸哪一个零件的 问题 ,而且随着产品的零件个数的增多 ,这样的拆卸路径个 数会产生组合爆炸。