阶梯气隙合愉罩极电动机的参数计算问题

有关阶梯气隙罩极电动机的文献已有许多 ,对 阶梯气隙的处理有下述几种方法:

( 1) 卡特系数法,这种方法象处理定子、转子的开槽影响一样 处理阶梯气隙 ,用相应的均匀气隙等效原来的非均 匀气隙;

( 2) 谐波磁导法 ,根据气隙磁场的观点 , 先计算出气隙的谐波磁导 ,然后计算各绕组产生的 磁势的作用;

( 3) 分相法  ,利用 Cha ng的等效原理,将极面分成几相 ,每相上有相应的等效绕组 , 阶梯气隙部分单独作为一相来处理;

( 4) 假想短路绕组法 ,在阶梯气隙上假想有一个短路绕组 ,将 阶梯气隙等效成均匀气隙 ,短路绕组的漏抗与阶梯 气隙的增加部分的磁阻有关 ,而其电阻为零。此外 , 还有改变主极跨距等其它方法。

虽然方法很 多 ,但所得结果并不能令人满意。究其原因 ,对由于 阶梯气隙产生气隙磁场畸变而引起的电机感抗参 数的变化没有准确的计算是一个十分重要的因素 , 另外罩极槽开口对气隙磁场波形的影响也是不容 忽视的问题。本文就这些不引人注意、然而又具有 根本性的问题进行探讨 ,以期引起在罩极电机的分 析和设计中对这方面的注意。

考虑分析上的方便 ,下述假设是必要和可行 的:

( 1) 电动机为线性装置 ,可以应用迭加原理;

( 2) 定子铁芯中各部分饱和程度的不均匀可以忽 略不计;

( 3) 电源电压随时间作正弦变化。

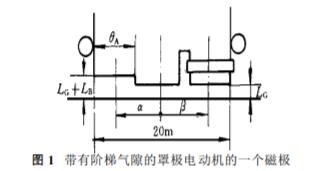
暂不考虑罩极槽对气隙磁场的影响。图 1是带 有阶梯气隙的罩极电动机的一个磁极。转子导条断 开时 ,罩极电机的电流与磁通相量图如图 2所示。 增加阶梯气隙后 ,由于气隙不均匀 ,气隙中的 磁场与均匀气隙磁场相比发生了畸变。阶梯气隙的 作用相当于在其位置上产生一个反向的附加磁场 分量 ,定子电流产生的穿过罩极匝的磁通 H′相应增加了 ΔH′,罩极匝中的感应电压 U2增大 ,感应 电流 I2随之增大 ,其产生的磁通 H″增加 ,因而罩极 相磁通 H2增加。

为了便于与均匀气隙的情况相比较 ,假设互磁 通增加的幅值为已知 ,只考虑基波情况时 ,定子绕 组和罩极匝之间的互感可以表示为

式中: M ′ 12为增加阶梯气隙后的互感; M12为均匀气 隙的互感; K1是互感增加的比例系数 ,其大小与阶 梯气隙的几何尺寸和选择磁场的波形有关 ,如果认 为磁场为图 3的方波 ,则

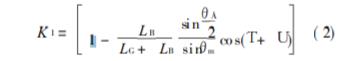
形状有关 ,磁通为理想方波时

K 2 = 1 2 2L G + LB LG + LB + L B L G + L B sin(θm - θα) sinθm ( 4)

由于主电抗下降 ,电机的功率因数降低。 同样的分析可以用于各次谐波参数的计算上。 值得指出的是: 由于罩极槽开口的影响和极尖边缘 效应以及铁芯饱和问题 ,参数的变化与上述的理想 情况有一定的差距 ,这将在后面作进一步的分析。

转子的曲折漏抗 X 2zm和斜槽漏抗 X 2sk与气隙 长度成反比 ,在不同气隙下转子导条的漏抗不同 , 但要准确地计算每根导条的漏抗并非明智之举 ,而 且不同气隙极面上的饱和程度的差别对消除导条 间的漏抗差别有利 ,因而在分析计算时 ,通常认为 它们完全相同。

以往的文献在分析中都没有对罩极槽开口对 气隙磁场的影响予以注意。实验测试结果表明: 罩 极槽开口对气隙磁场影响很大,因而在分析和 计算中必须计及。罩极槽为非对称性槽 ,且开口很 大 ,对气隙磁场的影响不适合用卡特系数方法来处 理 ,应根据磁场分析的计算结果选取适当波形来计 及其影响。 极尖处边缘效应的影响分有磁桥和没磁桥两 种情况。没有磁桥时 ,可根据电机磁场计算结 果 ,选取磁场波形;有磁桥时 ,边缘效应主要受 磁桥饱和程度的不同而发生变化 ,所以波形系数应 根据磁桥的不同饱和程度而适当选取 ,这要求在计 算磁桥漏抗的同时应考虑边缘效应。给出一些标准 样机的波形系数是需要进一步做的工作。 阶梯端边效应对气隙磁场的影响 ,可利用许克变换进行分析 B = Bmax w + L G LG + L B 2 w + 1 1 /2 ( 5) z 平面与 w 平面的关系较为复杂 ,在此省略。 上述三个因素对气隙磁场的影响 ,可根据式 ( 5)及电机磁场计算结果 ,然后进行适当的线性 化来处理。 磁路饱和问题是一个比较棘手的问题 ,当考虑定子主电抗的变化 增加阶梯气隙后 ,定子主电抗也由于气隙磁导 的改变而降低 X ′ m = K2X m ( 3) 式中: X ′ m 为采用阶梯气隙后的主电抗 , X m为均匀 气隙时的主电抗。减少的比例系数 K2与磁极几何饱和影响时 ,可以参考文献 的计算结果进行类 比处理 ,更好的方法是用有限元方法直接计算 ,但 这已不是建模参数计算的讨论范围了。 4. 2磁场波形系数的选取 由于阶梯气隙的影响 ,极面下的气隙磁场存在 正弦分量B (θ) = n=∑1, 3, 5… (Bcn cosnθ+ Bsn sinnθ)Bδcoskt ( 6) 当不考虑罩极槽开口的影响和极尖及阶梯端边边 缘效应 ,气隙磁场的波形如图 3所示Bcn = 2 nπ 2L G + LB LG + L B sinnθm + L B LG + L B sin(θm - θA ) ( 7) Bsn = 2L B nπ( LG + LB ) [co sn (θm - θA ) - cosnθm ] ( 8) 考虑罩极槽开口的影响和极尖边缘效应以及 阶梯端边效应 ,采用线性逼近后的气隙磁场波形如 图 4,相应的波形系数变为

分析有关文献 的计算结果可以得出: 当波形系数取两种磁场波形系数的平均值时 ,计算结果 更接近实测值。原因是多方面的 ,但磁场采用二维 计算与实际三维情况的差距肯定是一个重要的因 素。 采用变化后的参数建立的数学模型计算电动 机的性能并与实验结果比较 ,结果是令人满意的 , 这将在关于阶梯气隙罩极电动机的新数学模型的 文章中述及。